1. Graph
2. Properties of Graph
3. Non-trivial graph
4. Eulerian graph
5. Planar graph
6. Trees, Degree and Cycle of Graph
   1. Trees:

Graph

  Graphs consist of vertices (or nodes) connected by edges.

Formally, a graph is denoted as a pair $G(V, E)$.

Where $V$ represents the finite set vertices and $E$ represents the finite set edges.

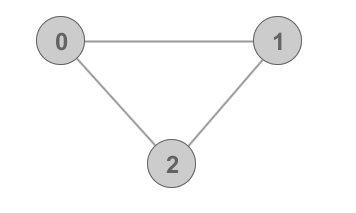
A basic graph of 3 cycle

(In the figure above, the vertices are the numbered circles, and the edges join the vertices.)

Properties of Graph

• The starting point of the network is known as root.
• When the same types of nodes are connected to one another, then the graph is known as an assortative graph.
• A cycle graph is said to be a graph that has a single cycle.
• When all the pairs of nodes are connected by a single edge it forms a complete graph.
• A graph is said to be in symmetry when each pair of vertices or nodes are connected in the same direction or in the reverse direction.
  When a graph has a single graph, it is a path graph.

Non-trivial graph

• A non-trivial graph consists of one or more vertices (or nodes) connected by edges.
• The degree of a vertex is the number of edges connected to that vertex.
• A graph in which it is possible to reach any vertex by traversing the edges from one vertex to another is said to be connected.
• The set of edges used (not necessarily distinct) is called a path between the given vertices.

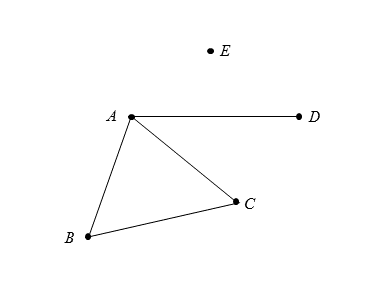
In the graph above, vertex AA is of degree 3, while vertices BB and CC are of degree 2. Vertex DD is of degree 1, and vertex EE is of degree 0.

Eulerian graph

• all of the edges are visited exactly once in a single path, known as an Eulerian path.

     Theorem: A Eulerian graph has at most two vertices of odd degree.
  

An analogous type of graph is the Hamiltonian path, one in which it is possible to traverse the graph by visiting each vertex exactly once.

Planar graph

A graph is said to be planar if it can be drawn on a flat plane without any of the edges crossing. If so, one can define a face of the graph as any region bounded by edges and containing no edges on the interior.

Euler's Formula

Suppose a planar graph has VV vertices, FF faces, and EE edges. Then

$V − E + F = 2$
$V − E + F =2$

Trees, Degree and Cycle of Graph

Trees:

A tree in a graph is the connection between undirected networks which have only one path between any two vertices. The graph trees have only straight lines between the nodes in any specific direction but have no cycles or loops. Therefore trees are a directed graph.

Degree: A degree is the number of edges connected to a vertex. It is denoted deg(v), where v is a vertex of the graph. It is the measure of the vertex.

Cycle: A cycle is a closed path in a graph that forms a loop. When the starting and ending point is the same in a graph that contains a set of vertices, then the cycle is formed. When there is no repetition of the vertex in a closed circuit, then the cycle is a simple cycle. The cycle graph is denoted by Cn.